Join me in the 2015 Reading Challenge!

Hi everyone!

Just a quick invitation to join me in the 2015 Reading Challenge! I decided to tackle this 50-line challenge at the beginning of the year, and each book I finish gets a mini-review posted on my Facebook page. “Like” me on Facebook to follow along as I dive headfirst into this ambitious attempt to read one book per week all year long!

If you want to join me, here are the rules:


  1. The 50 line items are detailed in the image below. You may choose to read one book per line item, or double up and check off as many items as apply to each book you read. I’m going for the super challenge of only assigning one line item per book.

  2. Either way, the goal is to have checked every item off the list by the end of 2015.

  3. EXTRA CHALLENGE BONUS RULE! I’m adding the bonus rule that each book must be one I haven’t yet read. I tend to do a lot of re-reading books as preparation for working with my students, but I was unsatisfied with the amount of new material I was reading. Completely optional, but bonus points if you do!

Here’s the list of items – get to reading!

by

Mathematical Journeys: Substitution Gone Wild and Opposing Coefficients: Systems of Equations, Two Ways

Settle in, folks, today’s a long one.

In The Function Machine, we learned that functions can be depicted as curves graphed on a coordinate plane. In What Does the Function Look Like?, we learned how to tell the general shape of a function’s graph based on characteristics of its equation, and vice versa. Today, we’ll be focusing on linear equations (meaning any equation that graphs into a straight line).

The defining characteristic of a linear equation is that the highest power of x in the equation is x to the first. This denotes that for every y value, there is exactly one corresponding x value. Of course, there is always exactly one corresponding y value for every x, but this is one of those “square is a rectangle; rectangle is not necessarily a square” moments. We know there’s exactly one y for every x because we choose our x’s independently and the y’s are dependent on them. There can’t be more than one y for any given x; you’ve only got one output slot in your machine. We don’t necessarily know that our y values won’t repeat, though, unless the function only has x to the first power and no higher.

So let’s look at a couple of linear functions. I’ll pick two at random.

y = 2x + 3
y = 6x – 5

Now, let’s think for a moment about how those two lines might relate to each other. There’s only a couple of ways a pair of lines can interact. They could be parallel, meaning that they never intersect. Parallel lines would have the same slope (you can find the slope as the coefficient on the x value in the equations above). These two lines do not have the same slope, so they’re not parallel.

If they’re not parallel, then by definition, they must intersect. And since they’re straight lines, they intersect at exactly one point. Let’s think for a moment about how we are able to graph equations in the first place. For a point to be on the line of an equation, that means that when you choose that point’s x value as your input, you get that point’s y value as your output. The x and y values of that point, plugged in to the equation, would make it true.

Well, if the two equations above intersect, then that means there’s exactly one point where the same set of x and y values would make both of these equations true at the same time. That sounds like something that’d be handy to know, huh? Wonder how we could do it…

What we’ve got here is known as a system of equations. That just means a set of more than one equation that we’re looking at together. And finding that intersect point requires what we refer to as “solving the system.” There are a couple of ways to do it – we’ll just look at the two most common.

Method 1: Substitution Gone Wild

We’ve already established that if you have a given value for one of the variables, you can plug that value in for that variable in an equation to find the remaining one. Extrapolate that – if you can substitute individual values for a variable, why couldn’t you substitute whole expressions in for variables, if you happened to know an appropriate one? Well, turns out you can. Let’s look at our equations again.

y = 2x + 3
y = 6x – 5

Now, the first step to substitution is to solve one of these equations for one variable. They’re both already solved for y, but for the sake of demonstration, I’m going to solve the first one for x.

y = 2x + 3
y – 3 = 2x
½ y – 3/2 = x

So now we have x in terms of y. Let’s take that newly-found expression and substitute it in for x in the other equation.

y = 6x – 5
y = 6(½ y – 3/2) – 5

Now we have an equation with only one variable in it. THAT we can solve to get a number. So let’s do it.

y = 6(½ y – 3/2) – 5
y = 6/2 y – 18/2 – 5
y = 3y – 9 – 5
y = 3y – 14
14 + y = 3y
14 = 2y
7 = y

So y is 7. Now that we have that information, we can plug THAT back in to our first equation to find x. The trick with this method is very simple – ALWAYS SWITCH EQUATIONS! If you accidentally try to plug this number back into the equation you were just using, you’ll end up in an infinite loop, going around in circles and getting more and more frustrated. That or you’ll cancel all the variables out and end up with 7 = 7, which doesn’t help at all. Remember to keep switching back and forth. Back to the first equation we go!

y = 2x + 3
7 = 2x + 3
4 = 2x
2 = x

So the intersect point of these two equations is at (2, 7). That’s the value that makes both equations true at the same time.

I like this method for its simplicity and ease of use. But there is another method that’s pretty popular, and it all hinges on opposing coefficients.

Method 2: Addition/Elimination/Subtraction method – Opposing Coefficients

This method goes by many names. I prefer the Elimination method, because it tells you what you’re doing. The goal with this method is the same as the previous one – get one equation to only have one variable in it. But this time, we’re going about it a little differently.

The basic idea of the Elimination method is to figure out a way to get the two equations to have opposite coefficients on one of the variables, so that if you were to add all the terms in those two equations, you’d cancel out one of the variables entirely. It requires us to establish at the outset that a couple of math moves are legal:

1. That we can multiply an entire equation by a single constant, multiplying each term by that constant, and we won’t change the value of the equation itself. It’s just like creating equivalent fractions back in middle school; as long as you do the same thing to each term, you’re creating an equivalent equation that looks different so that we can work with it better.
2. That we can add two equations together, by adding corresponding terms, to create a new equation that will also be true. In practice we’ll be adding straight down in columns.

Let’s take a look at our equations again.

y = 2x + 3
y = 6x – 5

Okay, I see some potential here. If we were to multiply the first equation by -3, we’d end up with a -6 on the x that would cancel out with the positive 6 in the second equation. Let’s try it.

-3(y = 2x + 3) → -3y = -6x – 9, so

-3y = -6x – 9
+ y = 6x – 5
-2y = 0x – 14

So we now have zero x’s – they’ve cancelled themselves out. Let’s solve the remaining equation for y to see what we get.

-2y = 0x – 14
-2y = -14
y = 7

Same as before. That’s a good sign! Now, here’s the only tricky part. We have to keep switching equations, so we need to know which one we were technically using up there. Which equation were we actually using? Well, the way I think of it is this: we added the second to the first, but we didn’t DO anything to the second equation, so that one’s still fair game. Think of it as using the second equation as a key to unlock the first one. We haven’t actually worked with the key equation yet, just used it to unlock others. Let’s plug our new value for y back in to the key equation.

y = 6x – 5
7 = 6x – 5
12 = 6x
2 = x

So our point is (2, 7) – just like with the other method!

And if we put those two original equations into a graphing calculator, we get:


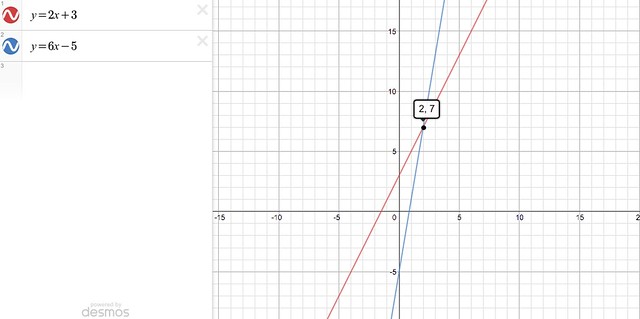
Thanks to Desmos Graphing Calculator for the image.

Well, fancy that!

To be honest, I’d rather use the substitution method. I think the process is simpler to remember, and with systems of equations, there are so many different ways to get from start to finish that I’d rather have a simple process I can remember than try to keep straight which equation is “active.” Plus, if Calculus is in your future it helps to learn the basic idea of substituting an expression in for a variable now, while it’s still relatively simple, so that later when you’re writing derivatives that stretch all the way across your notebook page you’ll have a more instinctive sense of how to accomplish the substitution part of it.

Elimination also has a tendency to turn into big ugly fractions – notice I chose coefficients for the terms that were both small and factorable? This is a nice, simple example, but math textbooks have a tendency to make problems unnecessarily complicated simply by using ugly numbers.

Speaking of which, stay tuned for next month’s Math Journey, when we tackle a big ugly system in three variables!

by

Ellen’s Choice: Why Does “Young Adult” Get A Bad Rap?

So-called “Young Adult” fiction seems to have gotten a bad rap lately among parents of teenage students. It seems as though adults tend to view YA as somehow “lesser” to other works, particularly as compared to the classics students are assigned in high school. I suspect this is because “Young Adult” as we conceptualize it today is a relatively recent invention – most bookstores and libraries didn’t even have a YA shelf until the mid-1990s. When we were teenagers, there was no “Young Adult” section at the bookstore – there was “Children’s” and there was “the rest of the store,” usually organized by genre. So as teens, too old for the Children’s section, we chose books from the rest of the store based on genre or author. I enjoyed sci-fi and fantasy, for example, so I found each next reading experience in the Sci-Fi/Fantasy aisle of the store, reading greats like Larry Niven, Neil Gaiman, and Isaac Asimov.

Young Adult, though, is a completely different animal. It’s a genre that’s not really a genre. The defining factor of a “Young Adult” novel is ill-defined, but tends to be simply “a book with a teenage main character.” Usually, although not always, a YA novel also deals with themes and concepts important to a teenage mind’s development, asking and attempting to answer big questions about life, love, identity etc. By that definition, a lot of the books we remember reading and enjoying as teens would probably be considered YA if they had been written today.

Phillip Pullman’s “His Dark Materials” trilogy, for example, is an alternate-universe fantasy epic seen through the eyes of a teenage girl. Its Wikipedia page lists it as YA (published in 1995), but it lives in the Sci-Fi/Fantasy section of my local bookstore, not the YA shelf. Gary Paulsen’s Hatchet, written in 1987, is a wilderness survival story also lumped under YA these days (though I know it wasn’t listed as such when I bought it originally in the ’80s). Lois Lowry’s classic dystopia The Giver (published in 1993) is listed as children’s, with a parenthetical clarification “generally Young Adult or older”. Clearly, this is not a well-thought-out system of classification.

The issue here is really that books fitting the above definition (“books with teenage main characters”) can be written in any genre. They can be realistic high school stories like Looking for Alaska and Paper Towns, magical boarding-school stories like Harry Potter or The Magicians, wilderness-survival stories or dystopias like the Hunger Games trilogy, or even feudal-era-Japanese-steampunk-dystopia-mythological-wilderness-survival-heroic-epics like the one I’m reading right now. (Stormdancer, by Jay Kristoff, in case you’re curious. Amazing so far.) The idea of a young person sorting out who they are and what they want out of life is not a new one, and is a timeless concept that can be transposed to any setting and trappings the author desires.

What Young Adult as a genre does have, though, is the potential to get teens really interested in reading. By definition, YA novels are written for teens. Skilled YA authors have developed a knack for writing from the perspective of a teenager, so their works resonate with teens more strongly than a classic might. YA stories also typically deal with problems that teens are dealing with themselves, at least on a conceptual level. Katniss Everdeen may live in a dystopian society where children are forced to fight to the death, but on a broader scale she is still dealing with the problems all teens are – how to take control of her own life, how to take a stand in favor of something she believes in, and in fact how to figure out what she believes in in the first place. These are questions we all struggle with, and good YA literature attempts to tackle these questions head on from a perspective that teens can understand.

by

Ellen’s Choice: Pros and Cons of the SAT vs. the ACT

Back in the day, where you wanted to go to college dictated which standardized test you took. Colleges in the midwest generally required the ACT, while those on the coasts wanted the SAT. These days, the score conversions are commonplace enough that most colleges will accept either one. So how do you choose which one to take? Well, there are a few differences to keep in mind.

Format

Most of the differences between the tests are matters of format. The SAT is comprised of ten sections ranging from 12 to 35 minutes each. The sections alternate between reading comprehension, math, and writing, and the whole test begins with a 25-minute timed essay. One of the ten sections is an “experimental” section, which is not scored as part of your test and is a chance for the test-makers to try out new ideas on a group of students. The ACT, in contrast, is four 75-minute sections, one for each subject. The ACT does not include an essay, but it does include a “science” section (which is actually more about reading graphs and charts than it is about science).

Because of this, a student’s ability to focus might lean them towards one or the other. A common problem for SAT students is not being able to finish each section in time or having trouble switching topics so frequently, so if that sounds like you, you might consider trying out the ACT. The ACT on average gives you less time per question, but by putting all of the questions of a given subject into a single section it gives you more time to get into the groove of the subject. This makes the ACT a better choice for students who need longer stretches of time to do good work, while students with attention problems might do better on the SAT where the constant subject-switching will keep them alert.

Another format difference is the style of the ScanTron sheet itself. The SAT’s questions have five answer choices, labeled A, B, C, D, and E, while the ACT’s questions have four answer choices that alternate between A, B, C, D, and F, G, H, J. The ACT’s system can make it easier to keep from accidentally bubbling in the wrong question number, since if you picked A as your answer and the bubble says F, you know you’re in the wrong line. However, having longer sections means there’s more chance of filling in the wrong lines in the first place, as you’ll be bouncing around the section for longer. Some books recommend figuring out your answers on scratch paper and then transferring them to the ScanTron in groups of five, which would help avoid that danger. However, it does complicate the workflow a bit. Overall, the ACT requires you to be a lot more organized in your time-management and workflow strategies, while the SAT does most of that for you by giving you shorter sections.

Material

Overall, scoring well on the SAT is less about knowing the material covered and more about knowing the strategies behind finding the correct answer. The SAT is more of a logic test than anything else, but the ACT relies a little bit more on actual knowledge of the material. The ACT also covers a bit more material – ACT math topics range up through basic trigonometry, while SAT math only covers geometry and basic algebra. This makes it a bit easier to come straight at the problems on the ACT and treat them more like you would any other test in school, but you do have to remember more material, while on the SAT you can often figure out the correct answer without even knowing the material itself.

A quick note: The SAT is undergoing a huge redesign in spring of 2016, and one of the changes that has been announced is a move towards more knowledge-oriented test questions. This would make the material on the SAT closer to that on the ACT. Stay tuned for updates as the new test is revealed!

Scoring

The SAT takes away a quarter point for each incorrect answer, while the ACT simply gives zero points for incorrect. In practice, this means that blind guesses are penalized on the SAT but are a valid last-ditch strategy on the ACT. However, this is another thing that will change in the 2016 redesign; the SAT will no longer penalize for guessing. But if you’re taking the test before then, it’s definitely something to keep in mind. Once again the ACT requires a bit more self-motivated workflow, as the best strategy here involves taking one last trip through each section in the last two minutes to bubble in all of your wild guesses. In a longer section it can be tricky to remember to save time for that.

In general the ACT leaves much more of the planning and strategy up to the student, while the SAT helps you along a bit through its format. My advice is usually to take a practice test for both and see how you do. Don’t just look at your scores, though – think about how it felt to take each test. Were you panicking at the end of each SAT section because you ran out of time? Then maybe the ACT is for you. Were you fuzzing out in the middle of the marathon ACT sections and having trouble staying focused? Then maybe you should try the SAT instead.

Also, since the point of taking these tests is to get into college, be sure to do your research. Check out the colleges you’re interested in and see what they require for test scores. Most will take either test, but it doesn’t hurt to be sure. Also, some schools will allow you to submit individual subject scores from different test dates (the math from March and the reading from October, for example), while others need one complete test score from a single date. Some schools will tell certain degree candidates up front that they don’t care about a certain part, like an engineering department not caring about the writing section or a school not looking at the essay at all. (The essay is a particularly good example of this, as most schools require an admissions essay anyway and some will only care about that one.)

I tutor both SAT and ACT prep, so if you’re in need of some assistance don’t hesitate to contact me!

by

WyzAnt Wants To Know: 5 Tips to Keep Tutoring Fun

What are your 5 outside the box tips that help make your tutoring lessons fun?

1. Have a sense of humor about learning.

I like to use humor in my tutoring, to keep students engaged and interested in the material. I’ve found that it’s easy to zone out during a lesson, and the classes I’ve retained the most information from myself have been ones where the teacher employed humor. In a writing class, a teacher explained the importance of context to spelling with the quip “You need to remember which witch is which, or you’ll suddenly have a lady with a black hat appear in your paper.” My high-school calculus teacher helped us remember the SOH-CAH-TOA trig function sequence by telling us a long joke about a native american who stubbed his toe and was advised by the village elder to “Soak-a-toe-a.” And later on, in a materials science class in college, our professor explained the molecular physics properties of a certain material with a joke about coal trying to rob aluminum by saying “This is a stick-up. Give me all your oxygen,” and the aluminum responding with “Yeah, you and who else?”

Not only are students more likely to retain information because they’re paying attention for the humor, but it also helps to keep the atmosphere in a session light. For me, learning is something to be enjoyed and to get excited about, and all too often people start to stress and become far more worried about their grades than about learning the material. If I can lighten the mood with a quip or a bad pun, if I can get that smile to cross the student’s face, then I’ve just associated learning and our lessons with a fun chat with a friend, and they’re more likely to come to future lessons with a motivation to learn.

2. Explain it back to me

One of my top strategies for working one-on-one with students is to have them explain a concept back to me. This works particularly well with math; if they know it well enough to explain it to someone else, then it’s not as much of an issue to remember it themselves. It also helps remind them of the upper-layer “concept” behind the process; saying “I need to do the Lowest Common Denominator thing” isn’t nearly as informative as “I need the denominators to be the same so I can add them, so I need to find a number that will divide by both of these denominators.”

I also use this strategy with SAT prep students; if they can explain to me how they would solve the problem, they’ve done the bulk of the work already. I frequently spend sessions taking an SAT student through a section of problems, not asking for the answer, but asking for “Explain to me how you would go about solving this one.”

3. Learn from your students and show that their opinions have value

I use this one a lot with English Literature students. In my opinion, there is no such thing as a wrong answer in Literature studies. If we’re discussing themes or symbols, I always encourage my students to chime in with anything they’ve been thinking about while reading, even and especially if I haven’t brought it up myself. I had a student last year, reading A Doll’s House by Henrik Ibsen, introduce the idea of a symbol I legitimately hadn’t even considered. She pointed out that in the third act, the Christmas tree – a definitionally useless ornamentation – was replaced by a lamp, a functional object. She connected this change to Nora’s changing mindset about becoming an adult and taking on the responsibilities of a human being. Nora was a useless ornamentation in the first part of the play, just like the Christmas tree, but now she’s seen the necessity of having a purpose. I was blown away by this quite articulate exploration, and I promptly encouraged her to delve deeper. By showing that I am willing to learn from my students, I let them know that their opinions have value and they should not feel self-conscious about sharing them.

4. Field Trips!

This one takes a bit of planning and doesn’t work with everyone, but if possible, I love to subvert the expected routine and take my student on a field trip of sorts. If it’s a nice day and I feel the student getting restless – why not work outside? If we meet up on Sunday and didn’t realize the library was closed – why not head to a nearby coffee shop and work there? If she’s studying Shakespeare and the local theater company happens to be doing a Shakespeare play, why not arrange an outing to see it? (or at the very least, let her know it’s happening and strongly encourage her to go)

5. See your students as people

I gave one of my students a little present two weeks ago. No special reason; I just felt like she’d been in a dreary mood the past few weeks and needed a little pick-me-up. Mid-November is always a tough time for learning; it just seems like Thanksgiving break will never ever come. Her eyes lit up, and she was motivated and happy for the rest of the week. One of my middle-school students had a birthday, and her dad canceled her lesson for that day so they could take her to the mall to get her ears pierced. The following lesson I brought her a birthday present – a pair of pierced-ear earrings. She stuck them in her backpack and flounced off with a broad smile on her face.

Sometimes, all a student needs is a little reminder that I know they’re a person with their own issues or excitements. I try to recognize that in my students, and keep an eye out for when they might just be having a rough week. Sometimes the student just needs an excuse to shake off the stress and get back to what they love. I can always tell with one of my students when she’s in a funk and doesn’t want to work, and usually I’ll indulge her with a few minutes of chatting about her favorite books.

6. Break down the authority dynamic

I just thought of another one, so consider this your bonus tip. I made a conscious choice when I started tutoring to come to lessons dressed simply in jeans and T-shirts. I always make sure I look presentable, but I don’t get dressed up to “business casual” or something similar when I tutor. This is deliberate, and is an attempt on my part to communicate a few things subconsciously.

First, I don’t want my students to see me as an authority figure in the same way that they see their parents or teachers. I would rather they see me as approachable, as a friend they can turn to with questions. I tell my students to think of me as someone who is here to help them, someone they can ask questions and run ideas past without having to worry about bad grades or punishments. I prefer to present myself on the same level as the student, here to help them figure something out, to share in their frustrations or confusions and see if I can shed some light on the problems they’re having. Dressing on the same level as them helps to communicate that.

A lot of times, especially with late middle-school or high-school students, the student-parent dynamic is already strained. I want to stay out of that dynamic, from the student’s point of view, as much as I possibly can. Often times, if a parent comes in with the student and chats with me about their performance before a lesson, I’ll listen and chat normally with the parent, while surreptitiously paying attention to how the student is reacting to their parents’ comments. (Oddly enough, parents will often talk to me as if their child isn’t present, or at the very least as if she can’t speak up for herself.) Then, once the parent has left and I’m alone with the student, I’ll turn to them and say, “So what do you think about that?” It’s natural for a parent to view their student as a child, even if they’re a senior in high school. I want the student to know that I see them as a responsible individual and am eager to hear what they have to say. My goal is for them to improve, so I want to hear what they’re not telling their parents. I want to be a friend who can help them with this, not yet-another-grown-up telling them what to do and what they’re doing wrong.

Second, I want to emphasize for my students that it doesn’t take a super-special person to be able to understand these topics, nor does it take special preparation to be able to execute them. You don’t have to get dressed up in a suit and heels in order to understand calculus; you just have to bring your brain and your desire to learn. If I can do it, so can you.

by

Mathematical Journeys: Subdivided Pie

Since it’s Thanksgiving week, let’s think about pie for a second. No, not mathematical pi, just actual real edible pies. For Thanksgiving I’m in charge of making dessert, so I’ll be bringing two pies, one pumpkin and one apple. Let’s say that I sliced the apple pie into 12 pieces, and the pumpkin pie, since it held together better, into 18.

Fast forward to the end of the evening. My pies were a big hit, and I have almost none left. In fact, all I have is three pieces of apple and four pieces of pumpkin. I want to combine the remaining slices into a single pie pan, so that they take up less space in the fridge. How do I figure out if my remaining pie will fit in one pan?

Well, let’s start by writing down the remaining amounts of pie in the form of fractions. Remember, one of the definitions of a fraction is parts of a whole, so let’s apply that definition to figure out our starting fractions.

The apple pie was cut into 12 pieces, and we have three out of twelve left. So our apple pie fraction is

 3
12

The pumpkin was cut into 18 pieces, and we have four left. So the pumpkin fraction is

 4
18

To figure out how much pie we have left and whether it will fit into one pan, we’ll have to add these two fractions together.

 3  +  4
12    18

Now, the first problem we run into is that our pies were cut into different amounts of pieces. We can’t accurately compare the two pies until we subdivide them into the same size pieces. So to do this, we’ll use a process that often confuses students when they first learn it: finding the Lowest Common Denominator.

I think this concept confuses students mostly because the terms used are long and complicated. So let’s talk about Lowest Common Denominator for a moment. We only specify Lowest because there are many different denominators that would work for this problem, but most of them are bigger than they need to be. We don’t want to work with numbers that are any larger than they need to be, so this process ensures that we don’t have to do any extra reducing after the fact.

We need to find a number that can divide evenly by both of our current denominators (though not necessarily at the same time). So all of the factors involved in either of our current denominators need to be present in our LCD. Let’s take the foolproof, long-way-round method and break each denominator down into its prime factors. You can do this with a factor tree:

12                18
3 x 4            3 x 6
3 x 2 x 2      3 x 3 x 2

So we see a lot of overlap here between the two denominators, right? Both contain a 3 and a 2. This is where the “lowest” part of the Lowest Common Denominator comes in. Worst case scenario, we could simply multiply each denominator by the other one and we’d come up with a number that both would divide by, right? But look at that overlap. That denominator might be common, but it certainly wouldn’t be the lowest – you’d be able to divide both top and bottom of each fraction by a 3 and a 2 (or by a 6, if you’re feeling efficient). We need all of those factors to be represented in the LCD, but we only need the duplicates to be represented once. What I like to do is rewrite the last lines of the factor trees one on top of the other, to make it easier to see the overlap:

12 =        3 x 2 x 2
18 = 3 x 3 x 2

So that 3 x 2 of overlap we only need once. So let’s rewrite out the prime factors that we need in our LCD:

LCD = 3 x 3 x 2 x 2

There. We have two 3’s, so the 18 will be happy, and two 2’s, so the 12 will be happy. What does that come out to?

LCD = 3 x 3 x 2 x 2 = 36

So our target number is 36. Now, let’s go back to our original problem:

 3 + 4
12  18

Now, remember that any number divided by itself is one? Good. And remember that one of the definitions of a fraction is a division problem you don’t want to do yet? Great. So we can multiply either of these fractions by a new fraction composed of a number over itself, and not change the actual value of the number. We’re simply rewriting it in a form that’s more useful to us. It’s basically the backwards application of the process for reducing a fraction. Only this time we’re not reducing; we’re making it more complex.

We’re going to do this in two separate cases. Just look at the first fraction for a moment. What number do we need to multiply the 12 by to get our target of 36?

If you’re stumped, just go back to the prime factor makeup of our target number and figure out what pieces are missing from the 12:

12 =           3 x 2 x 2
LCD = 3 x 3 x 2 x 2

So we’re missing a 3. So multiply that first fraction by 3/3, which, remember, is just a fancy way of writing “1”, so we can do that without messing up the value of the fraction:

3    x    3 =  9
12        3     36

Okay, good sign. Our denominator is 36, which was our target. Let’s take the second case. Look at the second fraction:

4
18

18 =     3 x 3 x 2
LCD = 3 x 3 x 2 x 2

So we’re missing a 2 here. Multiply by 2/2, which is just a fancy way of writing “1”:

4   x   2 = 8
18      2    36

Excellent! Hang on, we’re almost done. Now, what we’ve essentially found here are equivalent fractions for each of our originals that just happen to have the same denominator. Well, they don’t really “just happen” to have them; we did that on purpose to make our lives easier. So now we just plug these new forms of each fraction into the original problem:

9  +  8
36    36

And we have our pies subdivided into the same size pieces! Now we can add them normally to figure out if we have less than a whole pie’s worth of leftovers:

9   +   8 =    17
36    36       36

17 is less than 36, so we have less than a whole pie. We can safely put them both in the same pan without overflow.

Now if I could just figure out how to fit that turkey in the fridge…

by

Literature Spotlight: Appearances Deceive

War of the Worlds, by H.G. Wells, is classic science fiction. Written in 1924, it depicts the catastrophic and totally unexpected near-extinction of humanity by aliens from Mars. One of the main themes running through War of the Worlds is the idea that mankind’s assumptions about their world, the universe and the nature of life are constantly being challenged. The main reason the martians’ landing is so catastrophic to humankind is because the humans, by and large, have been lulled into a false sense of security. They believe they are capable of overcoming anything, that they are the most powerful beings in the universe, and as such are completely unprepared for the martians’ attack.

Humans at the beginning of H.G. Wells’s novel are portrayed as very self-satisfied. Even when confronted with the landing of the first martian cylinder, humanity is quick to dismiss the event as a mere curiosity. The story on the eve of the first day was “dead men from Mars,” (P. 14) and villagers from the area headed to the commons to see the cylinder as if it were a sideshow attraction. Almost immediately they are in over their heads and their assumptions are being proven wrong. The martians look nothing like humans, as everyone was subconsciously expecting them to. After this initial shock wears off, though, humanity quickly regains its mis-guided sense of security. The gravitational pull of earth is much stronger than the aliens’ native Mars, and they are sluggish in the atmosphere. Seeing this humanity continues to maintain a smug attitude about it all, claiming with certainty that there is no way the martians can get out of their pit. It never occurs to anyone that, just as humans have built technology to compensate for their weaknesses, the aliens might have done so as well. The reveal of the “fighting-machines” and the Heat-Ray throw this assumption into chaos, as the martians begin to slaughter the humans with no more thought than we might have to stepping on an anthill.

Stepping on an anthill brings up another facet of this theme: War of the Worlds is full of imagery depicting the humans as insects under the martians’ feet. The artilleryman states that “It never was a war, any more than there’s war between man and ants.” (P. 238) This imagery emphasizes the power the martians seem to hold over humanity, and humanity’s inability to deal with them at all. After all, how would an ant colony retaliate against a bulldozer? This imagery also points out the idea that humans barely register the existence of insects, just as the martians must barely be registering the humans’ attempts at retaliation. The introduction of the black gas furthers this theme by bringing up fumigation imagery; the idea that the martians spread a noxious cloud of gas across the land, then use jets of steam to disperse the gas itself, is reminiscent of humans smoking out a wasp nest or any other unwanted infestation. This imagery reduces all the splendor of humanity to a mere nuisance, something that must be dealt with to make the planet livable for the martians.

Fueling this theme is the fact that the humans actually do begin to display animalistic behavior in the wake of the martians’ destruction. Houses are broken into and looted, morals are abandoned, and it becomes every man for himself. Even our narrator succumbs to these animalistic tendencies, in a powerfully-moving scene where he murders an insane companion to keep from being discovered by the martians. This scene shows just how precarious our position really is, and how little it takes to unseat even the most sturdy of morals. Seeing humanity’s reaction makes it practically unthinkable that they could have resisted even if they knew what they were up against.

This theme comes full circle when the final destruction of the martians comes not at the hands of humans, but of the lowest of life forms – bacteria. In essence, what humanity could not do, the common cold did. This further emphasizes the powerlessness of the humans – the martians would have perished regardless of what humanity did to stop them. They were taken out by an entirely different force, and so humanity doesn’t really have a role in this drama at all. You could remove all of the humans and the story would have played out in much the same way.

Despite this, though, War of the Worlds has a truly hopeful theme arise in its resolution. Throughout the novel there are descriptions of the sheer size of the martians’ fighting-machines that highlight the futility of fighting something so much larger. But the destruction of all-powerful aliens by microscopic organisms reminds us that size does not equal power, and that the smallest of beings can still have a crucial impact. It also reminds us not to judge based on appearances or assumptions, and to keep our hubris in check. For in the vastness of the universe there are bound to be thousands of species more powerful than us, but that does not mean we are powerless to fight them.

by

Literature Spotlight: Actions Speak Louder Than Words

Ragtime, by E.L. Doctorow, is a story about the American dream. Set in New York during the “period of Ragtime” between the turn of the 20th century and the beginning of World War I, Ragtime tells the story of three different families struggling to find their place in this new America.

Doctorow makes use of an unusual writing style in Ragtime. He eschews the use of quotation marks and line breaks during dialogue, making the visual appearance of the novel one of long, blocky paragraphs. In addition, Doctorow writes the novel in third person from the perspective of not one but all of the main characters, allowing us to see the innermost thoughts and feelings of everyone in the story in turn. The characters have various degrees of name specificity, ranging from simply “Mother” and “Father” to “Sarah” (nobody knows her last name) to “Coalhouse Walker Jr.” All of these stylistic decisions come together to make a surprisingly fluid novel where actions speak much louder than words.

One of the themes running through Ragtime is the begrudging nature of the tolerance given to ethnic minorities during the period. Prejudice is rampant, and often times what someone says is quite different from what they actually think. In such a society, actions are often a much better indicator of a person’s true feeling than their voiced opinions. By removing quotation marks Doctorow downplays the dialogue in the novel, to the point that the reader stops really listening to what the characters are saying and instead looks to their actions to find their motivation. When the firemen antagonize Coalhouse, they do it with pleasant smirks and genteel words that are obviously concealing the disgust and hatred beneath. The minute Coalhouse leaves his car unattended, the firemen set to work vandalizing it and making it unusable. Their actions show their true feelings about him, even when they deny touching the car upon his return. With no quotation marks their statements run together and the reader almost doesn’t notice they said anything at all; their words have no more visual significance than the rest of the narration.

Doctorow emphasizes this effect often by juxtaposing a character’s statements or thoughts with a frank description of their actions. While he does not overtly state the discrepancy for the reader, placing a specific action next to a contrasting comment or thought allows the reader to make that jump for themselves. Father stating that it made the most sense for the Captain to take only his (African-American) manservant with him on the final leg of the journey to the North Pole so that the discovery could be “his and his alone” speaks to the ingrained inequality of the time – having an African-American with you didn’t really count as having another person there. In the same way, the team of Eskimos who helped them get to the pole (and without whom the trip probably wouldn’t even have happened) are seen as not counting either. The group takes a picture at the pole, and it’s described as a group of figures so bundled up that you can barely see their eyes. Doubtless any explorers the Captain would show that picture to would probably completely ignore the other figures and only see the Captain himself.

Ragtime is a beautifully-woven story of different families coming together and learning from one another in an era of change. Doctorow’s writing style makes it surprisingly readable and engaging, and he leaves just enough implied to allow the reader to make the final leap themselves.

by

WyzAnt Wants to Know: Preparing for your first lesson

“What advice would you give students to prepare for their first session with a new tutor?”

This is a great question! Overall, I think the most important piece of advice I can give is to put some thought into exactly what you want to get out of your tutoring sessions. Many people come to tutoring simply because their grades (or test scores) are low, and they’re hoping that private tutoring can “fix” the problem. Which it probably can, but if that’s all you bring to the table then your tutor has to work that much harder to figure out exactly how to go about helping you.

Before you arrive at your first meeting, spend some time thinking about your classes. Which subjects in school do you feel most comfortable with, and which ones least comfortable? Think over your answers like a detective – what common themes do you see that could be the real root of the problem? Were you easily able to ace an open-ended, discussion-driven English class, but this year your teacher runs class like a lecture and isn’t as open to opinions that aren’t his own? Did you instinctively understand your math class when the teacher used humor to keep you engaged, but this teacher simply drones on and on and you can’t focus on the problems at hand? Do you have trouble with the figures and illustrations in geometry even though you aced the more analytical, linear algebra class? Think about the differences between your classes and see if you can pinpoint what makes it difficult for you to learn. Then bring this information to your new tutor to help them formulate a strategy.

It’s also a good idea to bring a sample problem for the tutor to help you with, just to see how they teach. I always try to work a miniature lesson into my first meeting with a new student, since tutoring is really all about explaining the concepts in a way that the student understands. Everyone teaches differently, and a good tutor should be able to respond to your reactions and explain things in a variety of ways until something clicks. If you like the tutor’s teaching style, you’ll be more likely to look forward to lessons and you’ll get more out of them.

Once regular lessons begin, my top piece of advice is to come prepared, and remember that your tutor is here to help you. If you are unprepared for a lesson, there’s not much your tutor can do. No tutor wants to feel like they’re just there to watch you do your homework. Come in to each lesson with at least one concrete idea of something you’d like to work on – it can be as simple as working through a few homework problems or reviewing for a math test, or talking about a theme in your current English book. If you got a quiz back and don’t understand why you missed a question, bring that in and ask about it. If you just can’t figure out a topic, bring your book and ask for a review. If you want some extra writing practice, ask for some prompts. But whatever it is, ask! Don’t be afraid to be direct about what you want – your tutor is there to help deepen your understanding of the material, so if you’re clear and upfront about what you don’t understand your tutor will know what to do.

And remember, there’s no shame in tutoring – often you find that all you really needed was someone to take the time to explain it differently!

by

Mathematical Journeys: Inverse Operations, or “The Answer is Always 3”

Four years ago, I posted this math trick on my blog.  Take a look at it, and at the end I’ll show you why it works!

~

Let’s play a game. I’m going to let you make up a math problem, and I will be able to tell you the answer from here. I can’t see what you’re doing, I’m not even in the same room as you, but I will still be able to tell you the correct answer.

Trust me. I’m a professional. Ready?

Okay. First, pick a number. It can be any number you wish, large or small. Now add 5 to that number. Got it? Okay, now double your new number (multiply by 2). Alright, now subtract 4 from the double.

Next, divide your new number by 2. Now, finally, subtract your original number from this new quotient. Got it? Okay. Here comes the cool part. Ready?

The answer is 3. Nifty, huh? What’s that? How’d I do it? Oh, magic.

Okay, okay, it’s not magic. The answer will always be 3, no matter what number you pick. Let’s illustrate this by writing it out as an algebraic expression.

Pick a number, any number. Since your number could be anything and is therefore a variable, we’ll call it b.

Add 5.

b + 5

Double that.

2(b + 5)

Subtract 4.

2(b + 5) – 4

Divide by 2.

[2(b + 5) – 4] / 2

Now subtract your original number.

([2(b + 5) – 4] / 2) — b

Okay, so let’s simplify this expression and see what we get.

([2(b + 5) – 4] / 2) — b

Let’s get that fraction out of there. Divide each term in the numerator by 2.

(b + 5) – 2 – b

That’s better. Now simplify that.

b – b + 5 – 2

5 – 2

3

See? It doesn’t matter what number you pick, because the variable cancels itself out at the end. The answer is always 3. Now, go forth and amaze your friends!

~

This game is a perfect example of the concept of inverse operations. Inverse operations are operations that cancel each other out; what I sometimes refer to as “undoing” each other. Addition undoes subtraction and vice versa, multiplication undoes division. Early in the problem you double your mystery number, and then later on you divide it by two. Those two actions cancel each other out – one makes the number larger and the other shrinks it back down.

In an algebraic equation, you can effectively move a term from one side of the equals sign to the other by performing the inverse operation to both sides. Y = x + 5 becomes y – 5 = x, which can tell you the value of x instead of y. Algebra, at its heart, is the process of using these inverse operations to rewrite an equation so that it tells you the piece of information you want to know.